Note

Generated by nbsphinx from a Jupyter notebook. All the examples as Jupyter notebooks are available in the tudatpy-examples repo.

Earth-Mars transfer window design using Porkchop Plots

Copyright (c) 2010-2023, Delft University of Technology All rigths reserved This file is part of the Tudat. Redistribution and use in source and binary forms, with or without modification, are permitted exclusively under the terms of the Modified BSD license. You should have received a copy of the license with this file. If not, please or visit: http://tudat.tudelft.nl/LICENSE.

Important

This example requires the tudatpy.trajectory_design.porkchop module. Please ensure that your version of tudatpy does include this module.

Summary

This example shows how the tudatpy porkchop module can be used to choose an optimal launch and arrival date for an Earth-Mars transfer. By default, the porkchop module uses a Lambert arc to compute the \(\Delta V\) required to depart from the departure body (Earth in this case) and be captured by the target body (in this case Mars).

Users can provide a custom function to calculate the \(\Delta V\) required for any given transfer. This can be done by supplying a callable (a function) to the porkchop function via the argument

function_to_calculate_delta_v

This opens the possibility to calculate the \(\Delta V\) required for any transfer accounting for course correction manoeuvres along a planned trajectory.

Structure

This example consists of 3 sections:

  1. The imports, where we import the required modules

  2. Data management, where we define the file where the porkchop data will be saved

  3. The porkchop itself, which will only be recalculated if the user requests it

Import statements

[ ]:

# Tudat imports
from tudatpy import constants
from tudatpy.interface import spice_interface
from tudatpy.astro.time_conversion import DateTime
from tudatpy.numerical_simulation import environment_setup
from tudatpy.trajectory_design.porkchop import porkchop, plot_porkchop

Environment setup

[ ]:

# Load spice kernels
spice_interface.load_standard_kernels( )

# Define global frame orientation
global_frame_orientation = 'ECLIPJ2000'

# Create bodies
bodies_to_create = ['Sun', 'Venus', 'Earth', 'Moon', 'Mars', 'Jupiter', 'Saturn']
global_frame_origin = 'Sun'
body_settings = environment_setup.get_default_body_settings(
    bodies_to_create, global_frame_origin, global_frame_orientation)

# Create environment model
bodies = environment_setup.create_system_of_bodies(body_settings)

Porkchop Plots

We proceed to define the departure and target bodies and the time window for the transfer,

[3]:

departure_body = 'Earth'
target_body = 'Mars'

earliest_departure_time = DateTime(2005,  4,  30)
latest_departure_time   = DateTime(2005, 10,   7)

earliest_arrival_time   = DateTime(2005, 11,  16)
latest_arrival_time     = DateTime(2006, 12,  21)

To ensure the porkchop plot is rendered with good resolution, we calculate the time resolution of the plot to be 0.5% of the smallest time window (either the arrival or the departure window):

[ ]:

# Set time resolution IN DAYS as 0.5% of the smallest window (be it departure, or arrival)
# This will result in fairly good time resolution, at a runtime of approximately 10 seconds
# Tune the time resolution to obtain results to your liking!
time_window_percentage = 0.5
time_resolution = time_resolution = min(
        latest_departure_time.epoch() - earliest_departure_time.epoch(),
        latest_arrival_time.epoch()   - earliest_arrival_time.epoch()
) / constants.JULIAN_DAY * time_window_percentage / 100

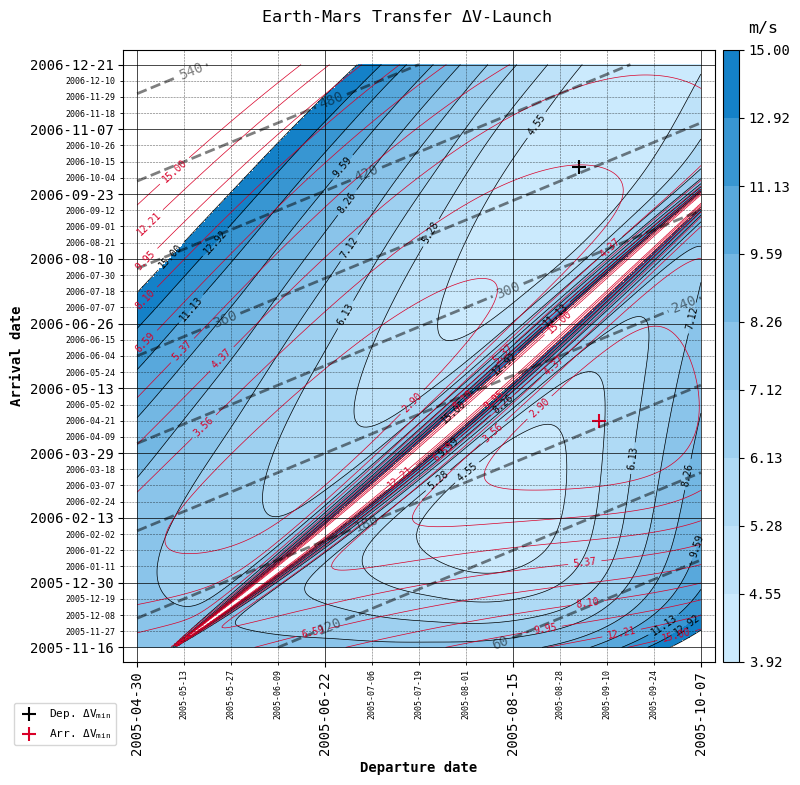
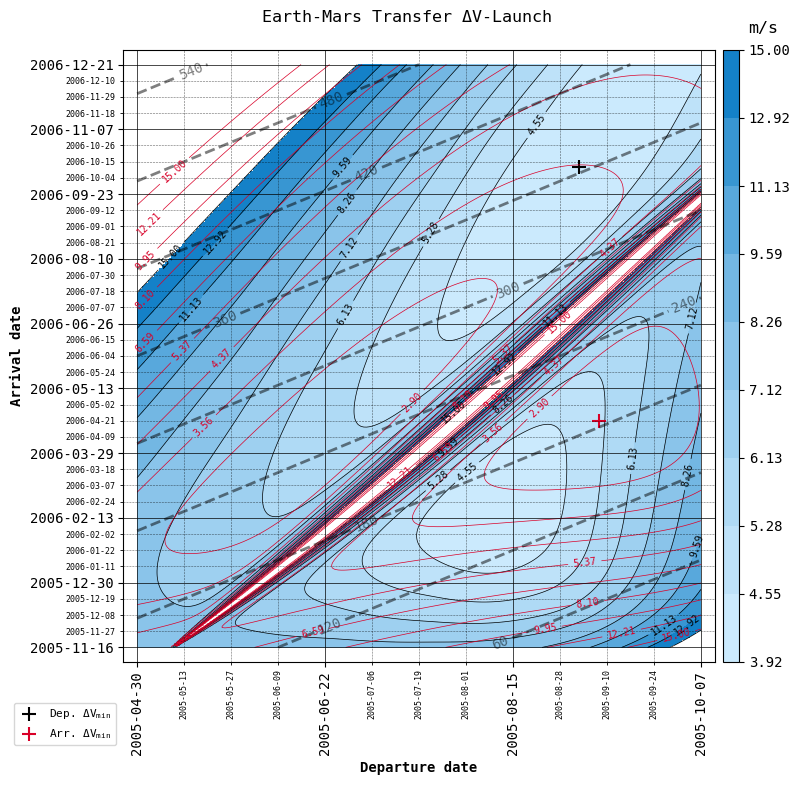
Lastly, we call the porkchop function, which will calculate the \(\Delta V\) required at each departure-arrival coordinate and display the plot, giving us

  • The optimal departure-arrival date combination

  • The constant time-of-flight isochrones

  • And more

[ ]:

[departure_epochs, arrival_epochs, ΔV] = porkchop(
    bodies,
    departure_body,
    target_body,
    earliest_departure_time,
    latest_departure_time,
    earliest_arrival_time,
    latest_arrival_time,
    time_resolution
)

Variations

The Tudat porkchop module allows us to

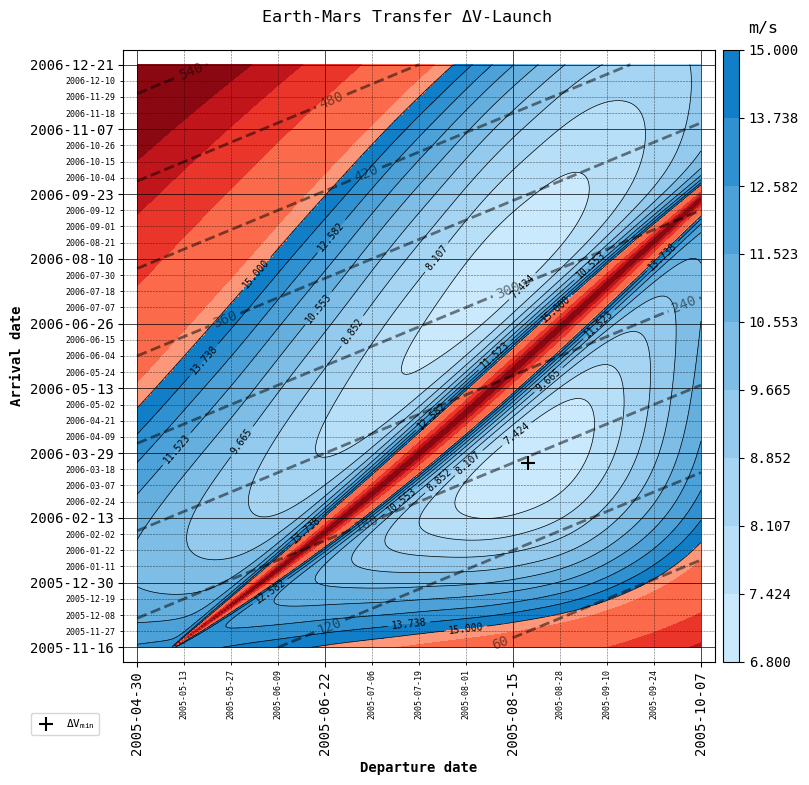
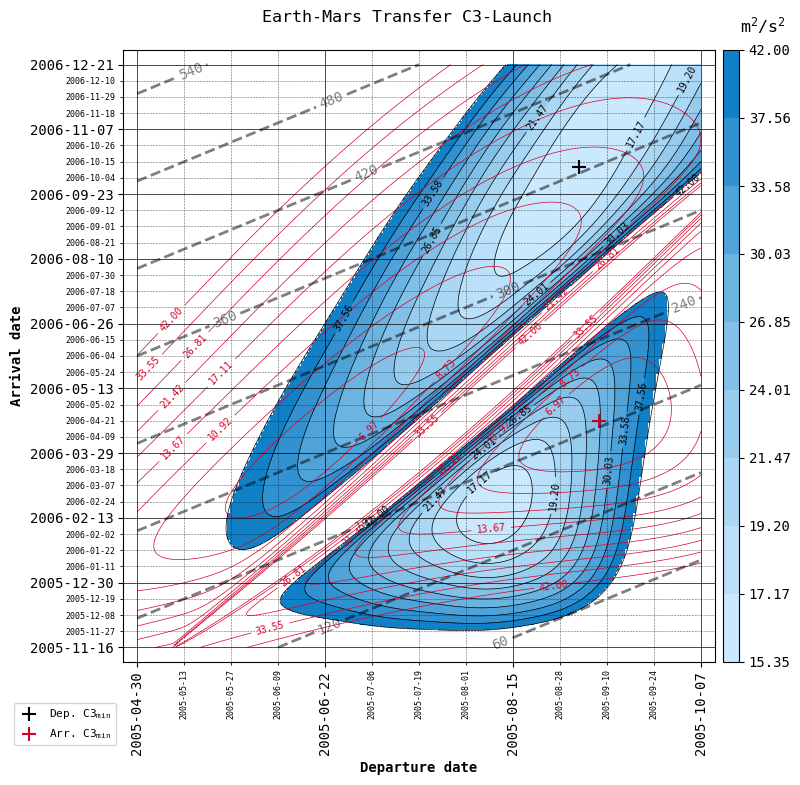
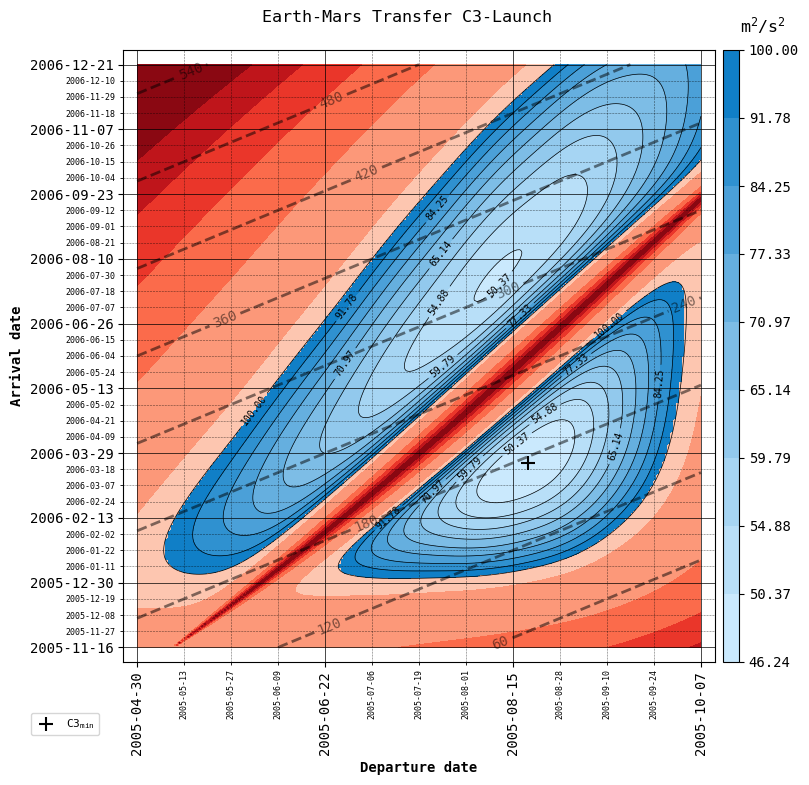
  • Save the \(\Delta V\) map returned by porkchop and plot it again without recalculating with the plot_porkchop function

  • Plot \(\Delta V\) (default) or C3 (specific energy), as well as choose whether to plot departure and arrival \(\Delta V\) together as the total \(\Delta V\) required for the transfer (default), or separately (in those cases in which the manoeuvre is performed in two burns, one at departure and one at arrival to the target planet).

Let’s make use of plot_porkchop to see all four combinations!

[ ]:

cases = [
    {'C3': False, 'total': False, 'threshold': 15 , 'filename': 'figures/ΔV.png'},
    {'C3': False, 'total': True,  'threshold': 15 , 'filename': 'figures/Δ_tot.png'},
    {'C3': True,  'total': False, 'threshold': 42 , 'filename': 'figures/C3.png'},
    {'C3': True,  'total': True,  'threshold': 100, 'filename': 'figures/C3_tot.png'}
]

for case in cases:
    plot_porkchop(
        departure_body   = departure_body,
        target_body      = target_body,
        departure_epochs = departure_epochs,
        arrival_epochs   = arrival_epochs,
        delta_v          = ΔV,
        save             = True,
        **case
    )