Note
Generated by nbsphinx from a Jupyter notebook. All the examples as Jupyter notebooks are available in the tudatpy-examples repo.
Hodographic-shaping MGA transfer optimization with PyGMO
Copyright (c) 2010-2022, Delft University of Technology. All rights reserved. This file is part of the Tudat. Redistribution and use in source and binary forms, with or without modification, are permitted exclusively under the terms of the Modified BSD license. You should have received a copy of the license with this file. If not, please or visit: http://tudat.tudelft.nl/LICENSE.
Context
This example illustrates the usage of PyGMO to optimize a low-thrust interplanetary transfer trajectory simulated using the multiple gravity assist (MGA) module of Tudat. The low-thrust legs are simulated using hodographic shaping. The spacecraft is considered to depart from the edge of the sphere of influence (SOI) of the Earth, execute swingbys at the Mars and Earth, and arrive at the edge of Jupiter’s SOI. Thus, the transfer includes 3 legs and 2 swingbys.
The velocity directions of each hodographic-shaping leg are modeled using the recommended shaping functions and two additional shaping functions, resulting in 2 velocity-shaping free coefficients per direction per leg (i.e. 6 per leg). Some simplifications are considered when defining the departure/arrival velocity at each transfer node: the angles defining the orientation of the arrival/departure velocity and the angles defining the orbital plane of a swingby are all assumed to take the value 0. Additionally, no impululsive \(\Delta V\) is considered to be applied during the swingbys.
The optimized parameters vector is consituted by the following variables: * Departure date (1 variable) * Magnitude of the departure excess velocity from Earth (1 variable) * Magnitude of the arrival excess velocity at Jupiter (1 variable) * Time of flight of each transfer leg (1 per leg, for a total of 3 variables) * Magnitude of the arrival excess velocity at each swingby planet (1 per swingby, for a total of 2 variables) * Altitude of the periapsis at each swingby (1 per swingby, for a total of 2 variables) * Leg free coefficients per leg (6 per leg, for a total of 18 variables) * Number of revolutions per leg (1 per leg, for a total of 3 variables)
Thus, a total of 31 variables is optimized.
The only objective function is the \(\Delta V\), which is minimized.
PyGMO is used in this example. It is assumed that the reader of this tutorial is already familiar with the content of this basic PyGMO tutorial.
Import statements
The required import statements are made here. Some standard modules are first loaded (numpy, matplotlib and typing). The pygmo and multiprocessing libraries are also imported. Then, the different modules of tudatpy that will be used are imported.
[1]:
# General imports
import numpy as np
from typing import List, Tuple
import pygmo as pg
import matplotlib.pyplot as plt
import multiprocessing as mp
# Tudatpy imports
import tudatpy
from tudatpy.util import result2array
from tudatpy import constants
from tudatpy.numerical_simulation import environment_setup
from tudatpy.trajectory_design import shape_based_thrust, transfer_trajectory
Helpers
First of all, let us define a helper function to create the MGA transfer object. Given some inputs, this function creates the transfer legs and nodes settings, and then uses them to create the transfer trajectory object. The function creates a transfer constituted by hodographic-shaping legs, selecting the shaping functions such that there are two free shaping coefficients per velocity direction per leg.
The function takes as inputs the usual parameters necessary for creating an MGA transfer object: the transfer body order, the departure orbit (semi-major axis and eccentricity), the arrival orbit (semi-major axis and eccentricity), the used system of bodies, and the name of the central body. Additionally, the function takes some more arguments used when defining the shaping functions: the time of flight per leg and the number of revolutions per leg.
The function returns the created transfer trajectory object.
[2]:
def create_low_thrust_transfer_object(transfer_body_order: list,
times_of_flight: np.ndarray,
departure_semi_major_axis: float,
departure_eccentricity: float,
arrival_semi_major_axis: float,
arrival_eccentricity: float,
bodies: tudatpy.kernel.numerical_simulation.environment.SystemOfBodies,
central_body: str,
numbers_of_revolutions: List[int]) -> \
tudatpy.kernel.trajectory_design.transfer_trajectory.TransferTrajectory:
# Create the list with the velocity shaping functions to use in each leg
radial_velocity_function_components_per_leg = []
normal_velocity_function_components_per_leg = []
axial_velocity_function_components_per_leg = []
for i in range(len(transfer_body_order)-1):
tof = times_of_flight[i]
frequency = 2.0 * np.pi / tof
scale_factor = 1.0 / tof
exponent = 4.0
radial_velocity_functions = shape_based_thrust.recommended_radial_hodograph_functions(times_of_flight[i])
radial_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_sine(
exponent=1.0,
frequency=0.5 * frequency,
scale_factor=scale_factor))
radial_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_cosine(
exponent=1.0,
frequency=0.5 * frequency,
scale_factor=scale_factor))
radial_velocity_function_components_per_leg.append(radial_velocity_functions)
normal_velocity_functions = shape_based_thrust.recommended_normal_hodograph_functions(times_of_flight[i])
normal_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_sine(
exponent=1.0,
frequency=0.5 * frequency,
scale_factor=scale_factor))
normal_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_cosine(
exponent=1.0,
frequency=0.5 * frequency,
scale_factor=scale_factor))
normal_velocity_function_components_per_leg.append(normal_velocity_functions)
axial_velocity_functions = shape_based_thrust.recommended_axial_hodograph_functions(
times_of_flight[i], numbers_of_revolutions[i])
axial_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_cosine(
exponent=exponent,
frequency=(numbers_of_revolutions[i] + 0.5) * frequency,
scale_factor=scale_factor ** exponent))
axial_velocity_functions.append(shape_based_thrust.hodograph_scaled_power_sine(
exponent=exponent,
frequency=(numbers_of_revolutions[i] + 0.5) * frequency,
scale_factor=scale_factor ** exponent))
axial_velocity_function_components_per_leg.append(axial_velocity_functions)
# Create the transfer leg and node settings
transfer_leg_settings, transfer_node_settings = transfer_trajectory.mga_settings_hodographic_shaping_legs(
body_order=transfer_body_order,
radial_velocity_function_components_per_leg=radial_velocity_function_components_per_leg,
normal_velocity_function_components_per_leg=normal_velocity_function_components_per_leg,
axial_velocity_function_components_per_leg=axial_velocity_function_components_per_leg,
departure_orbit=(departure_semi_major_axis, departure_eccentricity),
arrival_orbit=(arrival_semi_major_axis, arrival_eccentricity) )
# Create the transfer trajectory object
transfer_trajectory_object = transfer_trajectory.create_transfer_trajectory(
bodies,
transfer_leg_settings,
transfer_node_settings,
transfer_body_order,
central_body)
return transfer_trajectory_object
Optimisation problem
The core of the optimization process is realized by PyGMO, which requires the definition of a problem class. This definition has to be done in a class that is compatible with what the PyGMO library expects from a User Defined Problem (UDP). See this page from the PyGMO’s documentation as a reference. In this example, this class is called MGAHodographicShapingTrajectoryOptimizationProblem.
The following methods are implemented: * __init__(): This is the constructor for the PyGMO problem class. It is used to save all the variables required to setup the creation and evaluation of the transfer trajectory. * get_bounds(): Returns the bounds for each optimized parameter. These are provided as an input to __init__(). Their values are defined later in this example. * swingby_periapsis_to_optim_parameter(): When it comes to the swingby periapsis altitude, the parameter
that is optimized is the logarithm of the altitude, not the altitude itself. As such, this function converts the altitude to the optimized altitude parameter. This function can be modified to use a different scaling function (i.e. other than the logarithm). * optim_parameter_to_swingby_periapsis(): This function executes the inverse of the transformation done by the swingby_periapsis_to_optim_parameter function. That is, it converts the optimized altitude parameter to the periapsis
altitude. * get_nix(): Returns the number of design variables which are to be optimized as integers. In this case, the only integer parameters are the number of revolutions per leg. * get_transfer_trajectory_object(): For a given vector of design parameters, the function returns the evaluated transfer trajectory object. This is useful to further analyze the transfer after the optimization, allowing e.g. to retrieve the state history. * get_node_times(): For a given vector of
design parameters, the function returns the transfer node times. * fitness(): Returns the cost associated with a vector of design parameters. Here, the fitness is the \(\Delta V\) required to execute the transfer. Each time this function is called, a new transfer trajectory object is created and evaluated using the specified design parameters.
[3]:
#######################################################################
# Pygmo problem class
#######################################################################
class MGAHodographicShapingTrajectoryOptimizationProblem:
"""
Class to initialize, simulate, and optimize an MGA transfer with hodographic-shaping low-thrust legs.
"""
def __init__(self,
central_body: str,
transfer_body_order: List[str],
bounds: List[List[float]],
departure_semi_major_axis: float = np.inf,
departure_eccentricity: float = 0.0,
arrival_semi_major_axis: float = np.inf,
arrival_eccentricity: float = 0.0):
"""
Class constructor.
"""
self.transfer_body_order = transfer_body_order
self.central_body = central_body
self.no_of_swingbys = len(transfer_body_order) - 2
self.no_of_legs = len(transfer_body_order) - 1
# Number of free hodographic-shaping coefficients per leg, per velocity direction
# Currently the value is 2. Can be modified if the create_low_thrust_transfer_object function is changed in
# order to create hodographic legs with a different number of coefficients
self.no_free_shaping_coefficients_per_velocity_direction = 2
self.total_no_shaping_free_coefficients = self.no_free_shaping_coefficients_per_velocity_direction * 3 * self.no_of_legs
self.bounds = bounds
# Check if size of provided bounds is correct
if len(self.bounds) != 2 or len(self.bounds[0]) != 8 or len(self.bounds[1]) != 8:
raise RuntimeError("Size of provided parameters bounds is invalid.")
self.departure_semi_major_axis = departure_semi_major_axis
self.departure_eccentricity = departure_eccentricity
self.arrival_semi_major_axis = arrival_semi_major_axis
self.arrival_eccentricity = arrival_eccentricity
self.current_transfer_trajectory_object = None
self.current_node_times = None
self.current_design_parameter_vector = None
# Radius of solar system bodies, used to define the swingby periapsis radius.
#
# The values were retrieved from SPICE, using:
# from tudatpy.interface import spice
# spice.load_standard_kernels()
# bodies_to_create = ["Sun", "Mercury", "Venus", "Earth", "Mars", "Jupiter", "Saturn", "Uranus", "Neptune"]
# planetary_radii = {}
# for i in bodies_to_create:
# planetary_radii[i] = spice.get_average_radius(i)
self.planetary_radii = {
'Sun': 696000000.0,
'Mercury': 2439699.9999999995,
'Venus': 6051800.0,
'Earth': 6371008.366666666,
'Mars': 3389526.6666666665,
'Jupiter': 69946000.0,
'Saturn': 58300000.0,
'Uranus': 25363666.666666668,
'Neptune': 24623000.0 }
def swingby_periapsis_to_optim_parameter(self, swingby_periapsis) -> float:
"""
Converts the value of the swingby periapsis altitude to the parameter being optimized. The parameter being optimized
is the log10 of the periapsis.
"""
if swingby_periapsis <= 0:
raise RuntimeError(f"Value for the swingby periapsis altitude should be larger than zero (it is {swingby_periapsis}).")
return np.log10(swingby_periapsis)
def optim_parameter_to_swingby_periapsis(self, optim_parameter) -> float:
"""
Converts the value of the parameter being optimized to the swingby periapsis altitude. The parameter being optimized
is the log10 of the periapsis.
"""
return 10**optim_parameter
def get_bounds(self) -> Tuple[list, list]:
"""
Returns the bounds for the optimized parameters. For the integer parameters, the bounds should also be integers.
"""
################################################################################################################
# Extract user-defined bounds
# Departure date
departure_date_lb = self.bounds[0][0]
departure_date_ub = self.bounds[1][0]
# Departure velocity (departure from initial node)
departure_velocity_lb = self.bounds[0][1]
departure_velocity_ub = self.bounds[1][1]
# Arrival velocity (arrival to final node)
arrival_velocity_lb = self.bounds[0][2]
arrival_velocity_ub = self.bounds[1][2]
# Time of flight per leg
leg_time_of_flight_lb = self.bounds[0][3]
leg_time_of_flight_ub = self.bounds[1][3]
# Incoming velocity at swingby nodes
swingby_incoming_velocity_lb = self.bounds[0][4]
swingby_incoming_velocity_ub = self.bounds[1][4]
# Swingby periapsis altitude
swingby_periapsis_altitude_lb = self.swingby_periapsis_to_optim_parameter(self.bounds[0][5])
swingby_periapsis_altitude_ub = self.swingby_periapsis_to_optim_parameter(self.bounds[1][5])
# Free shaping coefficients of each leg
leg_free_coefficients_lb = self.bounds[0][6]
leg_free_coefficients_ub = self.bounds[1][6]
# Number of revolutions per leg
leg_number_of_revolutions_lb = self.bounds[0][7]
leg_number_of_revolutions_ub = self.bounds[1][7]
################################################################################################################
# Construct array with bounds of design parameter
# Select lower bounds
lower_bounds = []
lower_bounds.append(departure_date_lb)
lower_bounds.append(departure_velocity_lb)
lower_bounds.append(arrival_velocity_lb)
for _ in range(self.no_of_legs):
lower_bounds.append(leg_time_of_flight_lb)
for _ in range(self.no_of_swingbys):
lower_bounds.append(swingby_incoming_velocity_lb)
for _ in range(self.no_of_swingbys):
lower_bounds.append(swingby_periapsis_altitude_lb)
for _ in range(self.total_no_shaping_free_coefficients):
lower_bounds.append(leg_free_coefficients_lb)
for _ in range(self.no_of_legs):
lower_bounds.append(leg_number_of_revolutions_lb)
# Select upper bounds
upper_bounds = []
upper_bounds.append(departure_date_ub)
upper_bounds.append(departure_velocity_ub)
upper_bounds.append(arrival_velocity_ub)
for _ in range(self.no_of_legs):
upper_bounds.append(leg_time_of_flight_ub)
for _ in range(self.no_of_swingbys):
upper_bounds.append(swingby_incoming_velocity_ub)
for _ in range(self.no_of_swingbys):
upper_bounds.append(swingby_periapsis_altitude_ub)
for _ in range(self.total_no_shaping_free_coefficients):
upper_bounds.append(leg_free_coefficients_ub)
for _ in range(self.no_of_legs):
upper_bounds.append(leg_number_of_revolutions_ub)
return lower_bounds, upper_bounds
def get_nix(self):
"""
Select the number of integer parameters in the problem. The integer parameters are the last elements of the
design parameter vector. Here, only the numbers of revolutions per leg are considered to be integers.
"""
return self.no_of_legs
def get_transfer_trajectory_object(self,
design_parameter_vector: np.ndarray) -> \
tudatpy.kernel.trajectory_design.transfer_trajectory.TransferTrajectory:
"""
Function that creates a transfer trajectory object, evaluates it using the provided design parameter vector and
return the evaluated transfer trajectory object.
"""
if not (self.current_design_parameter_vector is not None and np.all(design_parameter_vector == self.current_design_parameter_vector)):
self.fitness(design_parameter_vector, post_processing=True)
return self.current_transfer_trajectory_object
def get_node_times(self,
design_parameter_vector: np.ndarray) -> \
tudatpy.kernel.trajectory_design.transfer_trajectory.TransferTrajectory:
"""
Function that creates a transfer trajectory object, evaluates it using the provided design parameter vector and
returns the associated node times.
"""
if not (self.current_design_parameter_vector is not None and np.all(design_parameter_vector == self.current_design_parameter_vector)):
self.fitness(design_parameter_vector, post_processing=True)
return self.current_node_times
def fitness(self,
design_parameter_vector: np.ndarray,
post_processing: bool = False) -> List[float]:
"""
Function to evaluate the fitness. A single-objective optimization is used, in which the objective is the deltaV
necessary to execute the transfer.
"""
# Compute the final index of each type of parameters
time_of_flight_index = 3 + self.no_of_legs
incoming_velocity_index = time_of_flight_index + self.no_of_swingbys
swingby_periapsis_index = incoming_velocity_index + self.no_of_swingbys
shaping_free_coefficient_index = swingby_periapsis_index + self.total_no_shaping_free_coefficients
revolution_index = shaping_free_coefficient_index + self.no_of_legs
################################################################################################################
# Extract floating point numbers from parameter vector
# Departure date
departure_date = design_parameter_vector[0]
# Departure velocity
departure_velocity = design_parameter_vector[1]
# Arrival velocity
arrival_velocity = design_parameter_vector[2]
# Time of flight per leg
times_of_flight = design_parameter_vector[3:time_of_flight_index]
# Incoming velocities at each swingby node
incoming_velocities = design_parameter_vector[time_of_flight_index:incoming_velocity_index]
# Swingby periapsis at each swingby node
swingby_periapse_altitudes = \
[self.optim_parameter_to_swingby_periapsis(x) for x in design_parameter_vector[incoming_velocity_index:swingby_periapsis_index]]
# hodographic shaping free coefficients
shaping_free_coefficients = design_parameter_vector[swingby_periapsis_index:shaping_free_coefficient_index]
################################################################################################################
# Extract integer numbers from parameter vector
# Number of revolutions
numbers_of_revolutions = \
[int(x) for x in design_parameter_vector[shaping_free_coefficient_index:revolution_index]]
################################################################################################################
# Create and evaluate the transfer trajectory
# Create the system of bodies
# This is done in the fitness function instead of the constructor so that the class can be pickled
bodies = environment_setup.create_simplified_system_of_bodies()
# Create the transfer trajectory object
transfer_trajectory_object = create_low_thrust_transfer_object(
self.transfer_body_order,
times_of_flight,
self.departure_semi_major_axis,
self.departure_eccentricity,
self.arrival_semi_major_axis,
self.arrival_eccentricity,
bodies,
self.central_body,
numbers_of_revolutions)
# Create the node times
node_times = []
node_times.append(departure_date)
for i in range(len(times_of_flight)):
node_times.append(node_times[i] + times_of_flight[i])
# Create the leg free parameters
leg_free_parameters = []
for i in range(self.no_of_legs):
leg_free_coefficients = np.array(shaping_free_coefficients[
i * self.no_free_shaping_coefficients_per_velocity_direction * 3 :
(i + 1) * self.no_free_shaping_coefficients_per_velocity_direction * 3])
leg_free_parameters.append([numbers_of_revolutions[i]] + leg_free_coefficients.tolist())
# Create the node free parameters
node_free_parameters = []
# Departure node parameters
# The excess velocity angles are taken to be 0.0
node_free_parameters.append([departure_velocity, 0.0, 0.0])
# Swingby nodes parameters
# The excess velocity angles, swingby plane angle, and deltaV are taken to be 0.0
for i in range(self.no_of_swingbys):
swingby_body = self.transfer_body_order[1:-1][i]
swingby_planetary_radius = self.planetary_radii[swingby_body]
swingby_periapse_radius = swingby_planetary_radius + swingby_periapse_altitudes[i]
node_free_parameters.append([incoming_velocities[i], 0.0, 0.0, swingby_periapse_radius, 0.0, 0.0])
# Arrival node parameters
# The excess velocity angles are taken to be 0.0
node_free_parameters.append([arrival_velocity, 0.0, 0.0])
# Evaluate the transfer and retrieve the delta V
try:
transfer_trajectory_object.evaluate(node_times, leg_free_parameters, node_free_parameters)
objective = transfer_trajectory_object.delta_v
# If in post-processing, save transfer trajectory object and node times
if post_processing:
self.current_design_parameter_vector = design_parameter_vector
self.current_transfer_trajectory_object = transfer_trajectory_object
self.current_node_times = node_times
else:
self.current_design_parameter_vector = None
self.current_transfer_trajectory_object = None
self.current_node_times = None
# If an error was thrown while evaluating the transfer, assign a very large value to the objective function
except RuntimeError:
objective = 1e16
# If in post-processing throw the error
if post_processing:
raise
# Return the value of the objective function
return [objective]
Optimization
Transfer Trajectory Setup
Before running the optimisation, it is first necessary to select some of the properties of the transfer trajectory: the central body, the sequence of bodies, the departure orbit, and the arrival orbit.
[4]:
if __name__ == '__main__':
###########################################################################
# Define transfer trajectory settings
###########################################################################
# Simplified bodies
central_body = 'Sun'
# Define order of bodies (nodes) for gravity assists
transfer_body_order = ['Earth', 'Mars', 'Earth', "Jupiter"]
# Define departure and insertion orbit
departure_semi_major_axis = np.inf
departure_eccentricity = 0.0
arrival_semi_major_axis = np.inf
arrival_eccentricity = 0.0
Optimization Setup
Next, the bounds of the optimized parameters are selected. The bounds used here were not tuned, therefore further tuning them might allow better optimization results to be found.
The lower and upper bounds for the departure and arrival velocities are all taken to have the value 0; as such, these free variables are not optimized.
[5]:
###########################################################################
# Select optimization bounds
###########################################################################
julian_day = constants.JULIAN_DAY
# Select bounds
departure_date_lb = 9000 * julian_day # s
departure_date_ub = 9200 * julian_day # s
departure_velocity_lb = 0.0 # m/s
departure_velocity_ub = 0.0 # m/s
arrival_velocity_lb = 0.0 # m/s
arrival_velocity_ub = 0.0 # m/s
leg_tof_lb = 200 * julian_day # s
leg_tof_ub = 1200 * julian_day # s
swingby_incoming_velocity_lb = 0 # m/s
swingby_incoming_velocity_ub = 7000 # m/s
swingby_periapsis_altitude_lb = 2e2 # m
swingby_periapsis_altitude_ub = 2e11 # m
leg_free_coefficient_lb = -1e4 # -
leg_free_coefficient_ub = 1e4 # -
leg_number_of_revolutions_lb = 0 # -
leg_number_of_revolutions_ub = 4 # -
bounds = [
[departure_date_lb, departure_velocity_lb, arrival_velocity_lb, leg_tof_lb, swingby_incoming_velocity_lb,
swingby_periapsis_altitude_lb, leg_free_coefficient_lb, leg_number_of_revolutions_lb],
[departure_date_ub, departure_velocity_ub, arrival_velocity_ub, leg_tof_ub, swingby_incoming_velocity_ub,
swingby_periapsis_altitude_ub, leg_free_coefficient_ub, leg_number_of_revolutions_ub]]
To setup the optimization, it is first necessary to initialize the optimization problem. This problem, defined through the class MGAHodographicShapingTrajectoryOptimizationProblem, is given to PyGMO trough the pg.problem() method.
The optimiser is selected to be the Simple Genetic Algorithm (SGA) algorithm (its documentation can be found here), and is created by calling pg.algorithm(). A fixed seed is used to ensure that the results are reproducible.
Since a large population is being optimized (1000 individuals), the pg.island class is used instead of pg.population. The island serves as a wrapper to the population, allowing the population to be evolved simultaneously in multiple threads, multiple processes, or even multiple machines. Here, as the type os island is not selected explicitly, usually the evolution will occur in multiple processes (though it depends on the operating systems), meaning that multiple CPUs will be used
simultaneously. A seed is also specified when creating the island (this seed is used when creating the initial population).
[6]:
###########################################################################
# Setup optimization
###########################################################################
seed = 42
pop_size = 1000
# Create Pygmo problem
transfer_optimization_problem = MGAHodographicShapingTrajectoryOptimizationProblem(
central_body, transfer_body_order, bounds, departure_semi_major_axis, departure_eccentricity,
arrival_semi_major_axis, arrival_eccentricity)
problem = pg.problem(transfer_optimization_problem)
# Create algorithm and define its seed
algorithm = pg.algorithm(pg.sga(gen=1))
algorithm.set_seed(seed)
# Create island
island = pg.island(algo=algorithm, prob=problem, size=pop_size, seed=seed)
Run Optimization
Finally, the optimization can be executed by successively evolving the island. To do so, the method island.evolve() is called the desired number of times inside a loop. After starting each evolution of the island, the method island.wait_check() is called, which makes the program wait for all the evolutions running in parallel to finish. After each evolution is finished, the best fitness and parameters vector are saved.
[7]:
###########################################################################
# Run optimization
###########################################################################
num_gen = 40
# Initialize lists with the best individual per generation
list_of_champion_f = [island.get_population().champion_f]
list_of_champion_x = [island.get_population().champion_x]
# freeze_support needs to be called when using multiprocessing on windows
# If called from other operating systems, freeze_support doesn't have any effect
mp.freeze_support()
for i in range(num_gen):
print('Evolution: %i / %i' % (i+1, num_gen))
island.evolve() # Evolve island
island.wait_check() # Wait until all evolution tasks in the island finish
# Save current champion
list_of_champion_x.append(island.get_population().champion_x)
list_of_champion_f.append(island.get_population().champion_f)
print('Evolution finished')
Evolution: 1 / 40
Evolution: 2 / 40
Evolution: 3 / 40
Evolution: 4 / 40
Evolution: 5 / 40
Evolution: 6 / 40
Evolution: 7 / 40
Evolution: 8 / 40
Evolution: 9 / 40
Evolution: 10 / 40
Evolution: 11 / 40
Evolution: 12 / 40
Evolution: 13 / 40
Evolution: 14 / 40
Evolution: 15 / 40
Evolution: 16 / 40
Evolution: 17 / 40
Evolution: 18 / 40
Evolution: 19 / 40
Evolution: 20 / 40
Evolution: 21 / 40
Evolution: 22 / 40
Evolution: 23 / 40
Evolution: 24 / 40
Evolution: 25 / 40
Evolution: 26 / 40
Evolution: 27 / 40
Evolution: 28 / 40
Evolution: 29 / 40
Evolution: 30 / 40
Evolution: 31 / 40
Evolution: 32 / 40
Evolution: 33 / 40
Evolution: 34 / 40
Evolution: 35 / 40
Evolution: 36 / 40
Evolution: 37 / 40
Evolution: 38 / 40
Evolution: 39 / 40
Evolution: 40 / 40
Evolution finished
Results Analysis
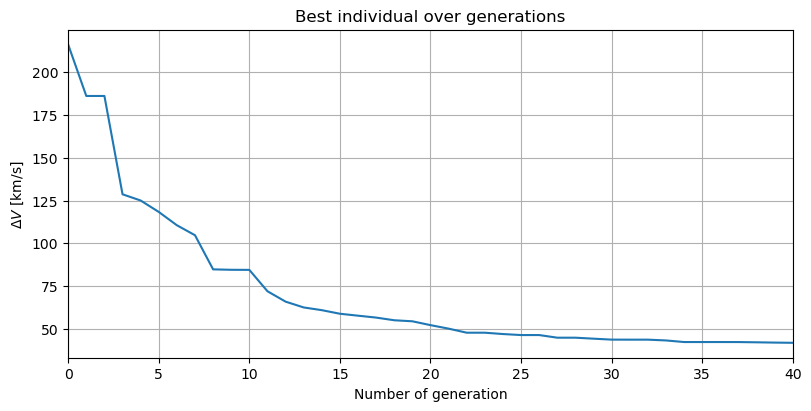
Having finished the optimisation, it is now possible to analyse the results. An optimum of 41.7 km/s was found, which is a very significant improvement with respect to the best fitness in the initial population (above 200 km/s). The evolution of the minimum \(\Delta V\) throughout the optimization is plotted.
[8]:
###########################################################################
# Extract the best individual and plot fitness evolution
###########################################################################
print('\n########### CHAMPION INDIVIDUAL ###########\n')
print('Total Delta V [m/s]: ', island.get_population().champion_f[0])
print("Parameters vector [various]: ", island.get_population().champion_x)
# Plot fitness over generations
fig, ax = plt.subplots(figsize=(8, 4), constrained_layout=True)
ax.plot(np.arange(0, num_gen+1), np.float_(list_of_champion_f) / 1000)
# Prettify
ax.set_xlim((0, num_gen))
ax.grid('major')
ax.set_title('Best individual over generations')
ax.set_xlabel('Number of generation')
ax.set_ylabel('$\Delta V$ [km/s]')
########### CHAMPION INDIVIDUAL ###########
Total Delta V [m/s]: 41742.274676065055
Parameters vector [various]: [ 7.81894702e+08 0.00000000e+00 0.00000000e+00 1.97844702e+07
6.68197546e+07 1.00154317e+08 4.15922786e+01 2.11897397e+03
8.70549952e+00 1.05640320e+01 -2.17914468e+03 -4.42585308e+03
-9.73639982e+03 4.99485513e+03 -8.57154454e+03 5.63559857e+03
-2.45927285e+03 8.18354031e+03 -6.81515208e+03 -4.95654244e+03
3.08336626e+03 -7.33231021e+03 -9.54212352e+03 8.77220874e+01
-9.22676384e+03 -9.51114116e+01 -7.02624208e+03 5.14620419e+03
0.00000000e+00 1.00000000e+00 0.00000000e+00]
[8]:
Text(0, 0.5, '$\\Delta V$ [km/s]')
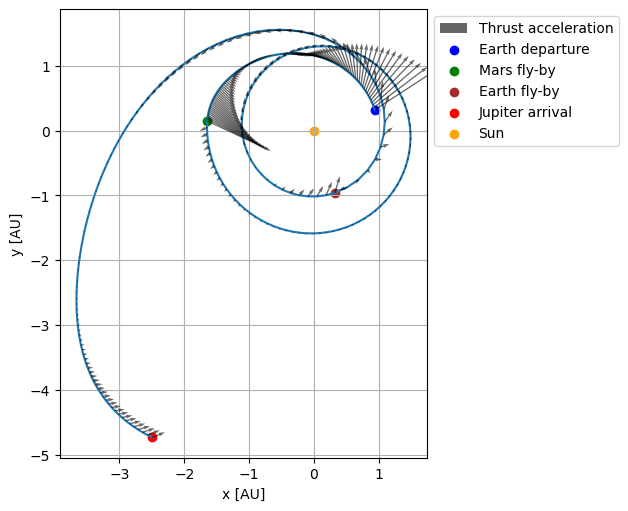
The transfer trajectory object associated with a given design parameter vector can be retrieved from the PyGMO problem class through the get_transfer_trajectory_object object. The returned object is already evaluated. Using the transfer trajectory object one can, for example, retrieve the state and thrust acceleration history throughout the transfer and plot them.
[9]:
###########################################################################
# Extract the champion trajectory object and plot trajectory
###########################################################################
design_parameters = island.get_population().champion_x
champion_transfer_trajectory_object = transfer_optimization_problem.get_transfer_trajectory_object(design_parameters)
champion_node_times = transfer_optimization_problem.get_node_times(design_parameters)
# Extract the state history
state_history = champion_transfer_trajectory_object.states_along_trajectory(100)
fly_by_states = np.array([state_history[champion_node_times[i]] for i in range(len(champion_node_times))])
state_history = result2array(state_history)
acceleration_history = champion_transfer_trajectory_object.inertial_thrust_accelerations_along_trajectory(100)
acceleration_history = result2array(acceleration_history)
au = 1.5e11
# Plot the state history
fig, ax = plt.subplots(figsize=(8,5), constrained_layout=True)
ax.plot(state_history[:, 1] / au, state_history[:, 2] / au)
ax.quiver(state_history[:, 1] / au, state_history[:, 2] / au,
acceleration_history[:, 1], acceleration_history[:, 2], label="Thrust acceleration", zorder=10, alpha=0.6)
ax.grid()
ax.scatter(fly_by_states[0, 0] / au, fly_by_states[0, 1] / au, color='blue', label='Earth departure')
ax.scatter(fly_by_states[1, 0] / au, fly_by_states[1, 1] / au, color='green', label='Mars fly-by')
ax.scatter(fly_by_states[2, 0] / au, fly_by_states[2, 1] / au, color='brown', label='Earth fly-by')
ax.scatter(fly_by_states[3, 0] / au, fly_by_states[3, 1] / au, color='red', label='Jupiter arrival')
ax.scatter([0], [0], color='orange', label='Sun')
ax.set_xlabel('x [AU]')
ax.set_ylabel('y [AU]')
ax.set_aspect('equal')
ax.legend(bbox_to_anchor=[1, 1])
[9]:
<matplotlib.legend.Legend at 0x1111aaaf0>